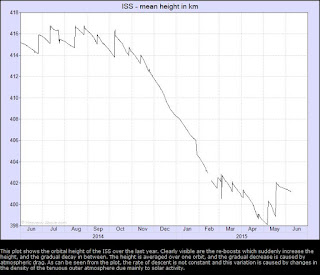
Here's a graph of the ISS altitude in 2014 and 2015 from http://www.heavens-above.com/
But, what makes astronauts drop to the floor of these tubes, the Earth side?
Cue Larry Niven. He wrote a pair of novels where humans crash "landed" into a huge taurus of smoke that orbited a star. Inside this Smoke Ring were things like oxygen, plants, predator, prey and Integral Trees. These were trees shaped like an integral sign used in calculus. At both ends of the tree it curved a bit, and in an opposite directions. Both ends were leafy, no obvious root system. These were air plants.

The benefit of this to humans was that microgravity allowed them to stick to the branches when sleeping, store items they built, set their baby down without fear of it floating away. The reason that Larry gave for this microgravity was that the orbital velocity of one end of the tree was less than the other end. But, the tree orbited at one velocity, obviously.

So, both ends of the tree were going the wrong speed. Any baby at the end of the tree closest to the star would tend to orbit more slowly than the tree, and therefore would be scooped up by the integral shape. At the opposite end, the baby tends to orbit faster, and would be scooped up by the integral shape on that end, which points in the opposite direction as the scoop at the other end.
So, an astronaut in the ISS is orbiting at the wrong velocity, probably. That's my guess. To find your gravity, use Newton's equation for gravitational force:
F = (G * M * m) / (r * r)
In physics and math, if the asterisk is not there, then it is assumed to be there. And a double carat is sometimes used for exponents.
F = G M m / r^^2
where F is the force, G is the gravitational constant (6.67E-11, which is notation for six point six seven times ten to the negative eleventh power), M is the bigger mass (like the star or the Earth), m is the smaller mass, like an integral tree or the space station, and r is the orbital radius.
You also need F = m * a, where a is your acceleration. Let one equation equal the other:
F = m a = (G M m) / (r r)
a = (G M) / (r r)
Since Earth's radius at the equator is 3,963 miles, and orbital altitude in low Earth orbit is between 200 and 300 miles for the ISS, then gravity at the altitude of the ISS is only a bit less than the gravity on the Earth. The difference is proportional to the inverse of the radius squared. We'll use 250 miles.
1 / (3,963 * 3,963) divided by 1 / (4,213 * 4,213) = 0.8848
So, the ISS experiences 88.48% of the gravity you feel in Ecuador (which is on the equator, which you can remember thanks to the spelling). On Earth's equator it's about 32.1 feet per second squared (sorry, just something I happen to know), so on the ISS it's about 28.4 fpss.
So, what's the difference between the ISS and an astronaut inside it? You need the distance in feet between the astronaut and the center of mass of the ISS. Heck, I don't know that. Looks like the astronaut is about ten feet closer to the Earth in this still from this video:
https://www.youtube.com/watch?v=T1hWJfsoiKw
That's 10/5280th of a mile, or about 0.0019 miles.
1 / (4,213 * 4,213) divided by 1 / (4,213.0019 * 4,213.0019)
This is the same as:
4213.0019^^2 / 4213^^2 = 1.0000009
And 28.4 times 1.0000009 is 28.40003, therefore Mike Massimino experienced an acceleration of 0.00003 feet per second squared. So, each second of time he accelerated 0.00003 feet. This is 0.008 millimeters per second. Hmmm... Looks about right in this video on how to brush your teeth in space. Watch the microphone float. It's really, really hard to see 0.008 mm of acceleration, isn't it?
https://www.youtube.com/watch?v=TU9kffoAQ8U
Looks like very little (or no) acceleration in this video of three guys floating around answering questions for the Google Plus hangout:
https://www.youtube.com/watch?v=Epdz2ySd3hE










No comments:
Post a Comment